Note
Go to the end to download the full example code
Modelling and Propagation of Legacy Petrophysical Data for Mining Exploration (3/3)¶
Modeling
Barcelona 25/09/24 GEO3BCN Manuel David Soto, Juan Alcalde, Adrià Hernàndez-Pineda, Ramón Carbonel
import dotenv
import os
Introduction¶
The dispersion and scarcity of petrophysical data are well-known challenges in the mining sector. These issues are primarily driven by economic factors, but also by geological (such as sedimentary cover, weathering, erosion, or the depth of targets), geotechnical (e.g., slope or borehole stability), and even technical limitations or availability that have been resolved in other industries (for instance, sonic logs were not previously acquired due to a lack of interest in velocity field data).
To address the challenge of sparse and incomplete petrophysical data in the mining sector we have developed three Jupyter notebooks that tackle these issues through a suite of open-source Python tools. These tools support researchers in the initial exploration, visualization, and integration of data from diverse sources, filling gaps caused by technical limitations and ultimately enabling the complete modeling of missing properties (through standard and more advanced ML-based models). We applied these tools to both, recently acquired and legacy petrophysical data of two cores northwest of Collinstown (County Westmeath, Province of Leinster), Ireland, located 26 km west-northwest of the Navan mine. However, these tools are adaptable and applicable to mining data from any location.
After the exploratory data analysis (notebook 1/3) and filling the gaps in the petrophysical dataset of Collinstown (previous notebook 2/3), this third notebook is focused on modeling by Machine Learning (ML) algorithms entire missing variables, such as the Gamma Ray (GR) measurement, which is available in only one of the petrophysical boreholes. The tasks to perform in this notebook are:
Load and merge the legacy GR data of borehole TC-3660-008 into its petrophysical dataset.
Use the merged data to train and evaluate different ML algorithms capable of predicting GR data in other boreholes.
By using the trained best model, propagate the GR to the other petrophysical borehole.
Evaluate the possibility of propagating this (GR) or other properties to other boreholes with less available data.
As with the previous notebooks, these tasks are performed with open-source Python tools easily accessible by any researcher through a Python installation connected to the Internet.
Variables¶
The dataset used in this notebook is the imputed dataset from the previous notebook (2/3), features3. It contains the modelable petrophysical features of the two available boreholes; TC-1319-005 and TC-3660-008. Hole (text object) and Len (float) variables are for reference, Form (text object) is a categorical variable representing the Major Formations:
Name |
Explanation |
Unit |
|---|---|---|
Hole |
Hole name |
|
From |
Top of the sample |
m |
Len |
Length of the core sample |
cm |
Den |
Density |
g/cm³ |
Vp |
Compressional velocity |
m/s |
Vs |
Shear velocity |
m/s |
Mag |
Magnetic susceptibility |
|
Ip |
Chargeability or induced polarization |
mv/V |
Res |
Resistivity |
ohm·m |
Form |
Major formations or zone along the hole |
The GR measurement from keyhole TC-3660-008 is the property we want to transfer to the other borehole, TC-1319-005. The challenge lies in the fact that both datasets have different ranges and intervals, and is not possible to make an ML model unless both datasets (new petrophysical features and legacy GR) are integrated into a single dataframe.
Libraries¶
The following are the Python libraries used along this notebook. PSL are Python Standard Libraries, UDL are User Defined Libraries, and PEL are Python External Libraries:
PLS
import sys
import warnings
#UDL
from vector_geology import basic_stat, geo
# PEL- Basic
import numpy as np
import pandas as pd
from tabulate import tabulate
import json
# PEL - Plotting
import matplotlib.pyplot as plt
# PEL - Filtering
from scipy.signal import butter, filtfilt
# # PEL - Data selection, transformation, preprocessing
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
# # PEL- ML algorithms
from sklearn.linear_model import LinearRegression, Lasso, Ridge
from sklearn.svm import SVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
import xgboost as xgb
# PEL - Metrics
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
from sklearn.metrics import make_scorer, mean_absolute_error, mean_squared_error
Settings¶
Activation of qt GUI Seed of random process
seed = 123
# Warning suppression
warnings.filterwarnings("ignore")
Data Loading¶
features3, imputed features, data load
features3 = pd.read_csv('Output/features3.csv', index_col=0)
features3.head()
features3.describe()
Columns in the features3
features3.columns
Index(['Hole', 'From', 'Len', 'Den', 'Vp', 'Vs', 'Mag', 'Ip', 'Res', 'Form'], dtype='object')
Imputed features of borehole TC-3660-008
features3_8 = features3[features3.Hole=='TC-3660-008']
features3_8 = features3_8.reset_index(drop=True)
features3_8
Depth information of feature3
print('Petrophysical features of TC-360-008', '\n')
print('Top:', features3_8.From[0])
print('Base:', features3_8.From[len(features3_8) - 1], '\n')
print('Length:', len(features3_8))
print('Range:', features3_8.From[len(features3_8) - 1] - features3_8.From[0], '\n')
print('First step: {:.1f}'.format(features3_8.From[1] - features3_8.From[0]))
# Mean step
steps = []
for i in range(len(features3_8) - 1):
steps.append(features3_8.From[i+1] - features3_8.From[i])
print('Mean step: {:.2f}'.format(np.mean(steps)))
Petrophysical features of TC-360-008
Top: 9.600000000000025
Base: 833.4
Length: 168
Range: 823.8
First step: 3.3
Mean step: 4.93
Legacy GR data of different holes
dotenv.load_dotenv()
base_path = os.getenv("PATH_TO_COLLINSTOWN_PETRO")
gr = pd.read_csv(f'{base_path}/collinstown_Gamma.csv')
gr.head()
Python-dotenv could not parse statement starting at line 13
Python-dotenv could not parse statement starting at line 14
Python-dotenv could not parse statement starting at line 15
Python-dotenv could not parse statement starting at line 16
Python-dotenv could not parse statement starting at line 17
Different holes in the legacy GR dataframe
gr.HOLEID.unique()
array(['TC-3660-007', 'TC-3660-008', 'TC-3839-002'], dtype=object)
Legacy GR of borehole TC-3660-008
gr8 = gr[gr.HOLEID == 'TC-3660-008'].reset_index(drop=True)
gr8
gr8.describe()
Depth information of the legacy GR
print('Legacy GR of TC-360-008', '\n')
print('Top:', gr8.DEPTH[0])
print('Base:', gr8.DEPTH[len(gr8) - 1], '\n')
print('Length:', len(gr8))
print('Range:', gr8.DEPTH[len(gr8) - 1] - gr8.DEPTH[2], '\n')
print('First step: {:.1f}'.format(gr8.DEPTH[3] - gr8.DEPTH[2]))
# Mean step
steps = []
for i in range(2, len(gr8) - 1):
steps.append(gr8.DEPTH[i+1] - gr8.DEPTH[i])
print('Mean step: {:.2f}'.format(np.mean(steps)))
Legacy GR of TC-360-008
Top: -0.2
Base: 830.8
Length: 8723
Range: 830.8
First step: 0.1
Mean step: 0.10
Data Merging¶
To model a new GR in borehole TC-1319-005, the legacy GR (gr8) and petrophysical data of borehole TC-3660-008 (feature3_8) have to be integrated into a single dataframe, free of NaNs.
Depth Equalization¶
The first step in merging the process of the legacy GR into the petrophysical data of borehole TC-3660-008 is to equalize the depths of both dataframes by the use of conditional expressions:
Equalizing depths in feature3
features3_8 = features3_8[features3_8.From <= 830.8].reset_index(drop=True)
features3_8
New depth information of feature3
print('Petrophysical features of TC-360-008', '\n')
print('Top:', features3_8.From[0])
print('Base:', features3_8.From[len(features3_8) - 1], '\n')
print('Length:', len(features3_8))
print('Range:', features3_8.From[len(features3_8) - 1] - features3_8.From[0], '\n')
print('First step: {:.1f}'.format(features3_8.From[1] - features3_8.From[0]))
# Mean step
steps = []
for i in range(len(features3_8) - 1):
steps.append(features3_8.From[i+1] - features3_8.From[i])
print('Mean step: {:.2f}'.format(np.mean(steps)))
Petrophysical features of TC-360-008
Top: 9.600000000000025
Base: 828.8
Length: 167
Range: 819.1999999999999
First step: 3.3
Mean step: 4.93
Equalizing depths in the legacy GR
gr8 = gr8[(gr8.DEPTH >= 9.6) & (gr8.DEPTH <= 828.8)].reset_index(drop=True)
gr8
New depth information of the legacy GR
print('Legacy GR of TC-360-008', '\n')
print('Top:', gr8.DEPTH[0])
print('Base:', gr8.DEPTH[len(gr8) - 1], '\n')
print('Length:', len(gr8))
print('Range:', gr8.DEPTH[len(gr8) - 1] - gr8.DEPTH[2], '\n')
print('First step: {:.1f}'.format(gr8.DEPTH[3] - gr8.DEPTH[2]))
# Mean step
steps = []
for i in range(2, len(gr8) - 1):
steps.append(gr8.DEPTH[i+1] - gr8.DEPTH[i])
print('Mean step: {:.2f}'.format(np.mean(steps)))
Legacy GR of TC-360-008
Top: 9.6
Base: 828.8
Length: 8605
Range: 819.0
First step: 0.1
Mean step: 0.10
Filtering and Dowsampling¶
Now that the depths of the legacy GR and the petrophysical data of borehole TC-3660-008 have been equalized, the next challenge is to merge the legacy GR into the petrophysical data. This involves condensing the 8605 legacy GR values into a new petrophysical feature with 167 values that can be used in the models. This task has been archived by combining a Butterwort filter and a downsampling function, an ideal combination for data with fast fluctuation such as the GR log (only downsampling produces a very spiky result). The effect of the filter, downsampling, and filter followed by downsampling can be appreciated at the end of this section.
Simplify the legacy GR
gr8 = gr8[['DEPTH', 'GeoPhys_NGAM_API']]
gr8
Rename series in the legacy GR
gr8 = gr8.rename(columns={'DEPTH':'depth', 'GeoPhys_NGAM_API':'gr'})
gr8
Downsampling the legacy GR but keeping the first and last value
reduc = int((len(gr8)) / 165)
gr8_middle = gr8.iloc[1:-1].iloc[::reduc, :]
gr8_down = pd.concat([gr8.iloc[[0]], gr8_middle, gr8.iloc[[-1]]])
gr8_down = gr8_down.sort_values('depth').reset_index(drop=True)
gr8_down
Butterworth filter on the legacy GR
b, a = butter(N=2, Wn=0.02, btype='low')
filtered_gr = filtfilt(b, a, gr8.gr)
gr8['gr_fil'] = filtered_gr
gr8 = gr8.sort_values('depth').reset_index(drop=True)
gr8
Downsampling the filtered GR
gr8_fil_down_middle = gr8.iloc[1:-1].iloc[::reduc, :]
gr8_fil_down = pd.concat([gr8.iloc[[0]], gr8_fil_down_middle, gr8.iloc[[-1]]])
# Sort by depth
gr8_fil_down = gr8_fil_down.sort_values('depth').reset_index(drop=True)
gr8_fil_down
Plot of filter and/or downsampling
plt.figure(figsize=(15, 8))
plt.subplot(121)
plt.plot(gr8.gr, gr8.depth, label='Original')
plt.legend()
plt.grid()
plt.xlabel('GR (API)')
plt.xlabel('Depth (m)')
plt.axis([0, 120, 850, 0])
plt.ylim(850, 0)
plt.subplot(122)
plt.plot(gr8_down.gr, gr8_down.depth, label='Down Samplig')
plt.plot(gr8.gr_fil, gr8.depth, label='Butterworth Filtered')
plt.plot(gr8_fil_down.gr_fil, gr8_fil_down.depth, label='Butterworth Filtered & Down Sampling')
plt.legend()
plt.grid()
plt.xlabel('GR (API)')
plt.xlabel('Depth (m)')
plt.axis([0, 120, 850, 0])
plt.ylim(850, 0)
plt.suptitle('Borehole TC-3660-008 GR', y=0.98)
plt.tight_layout()
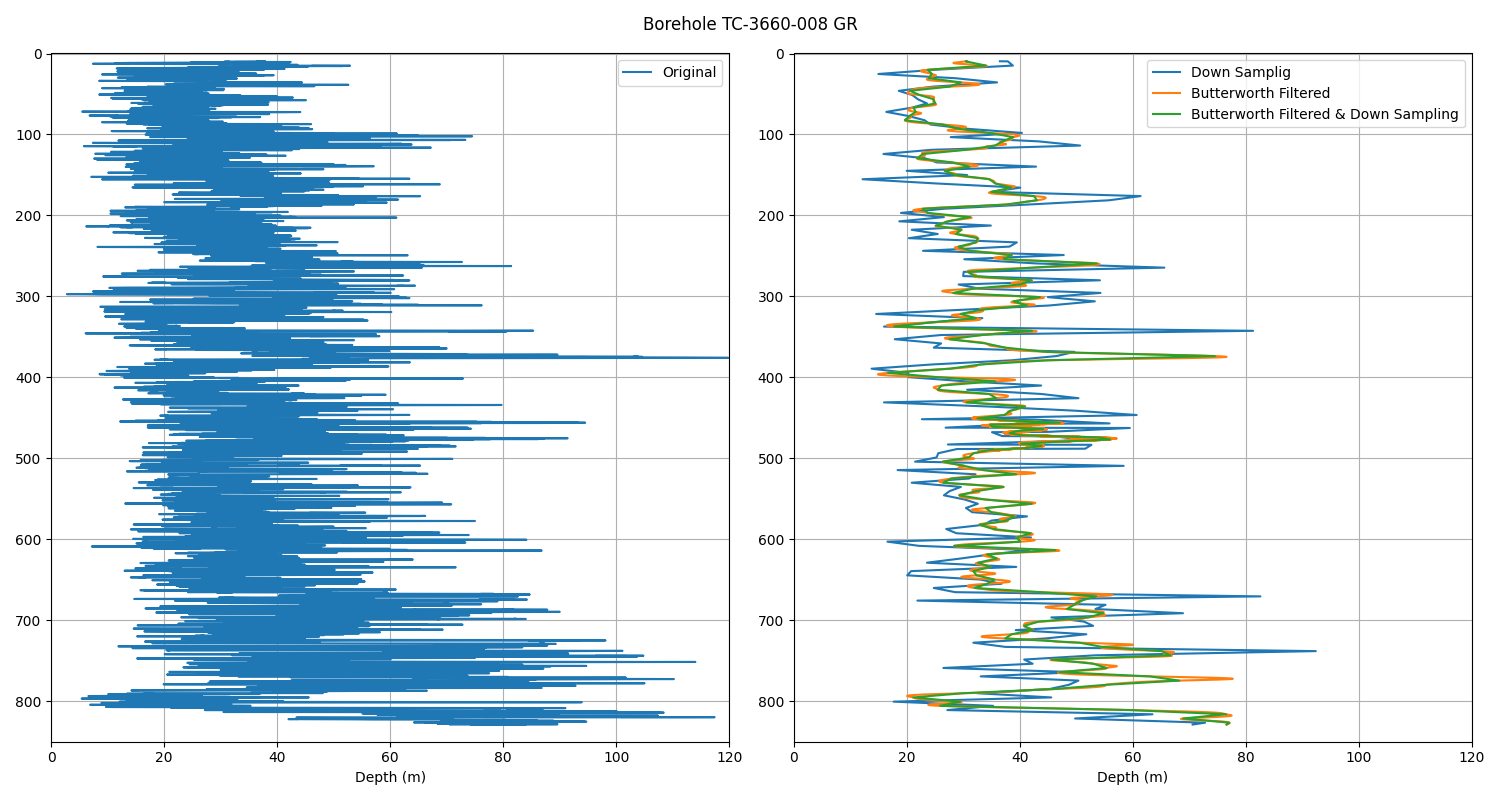
Integrated Dataframe¶
As the downsampling gave 168 values, we dropped the central value to reach 167 (the length of the petrophysical dataset) and then fused the filter and downsampled GR into the petrophysical data of borehole TC-3660-008.
Drop of central value in the filter and downsampled GR
del_index = len(gr8_fil_down)//2
gr8_fil_down = gr8_fil_down.drop(axis=0, index=del_index).reset_index(drop=True)
gr8_fil_down
Final integrated dataframe without NaNs
features3_8['GR'] = gr8_fil_down.gr_fil
features3_8
features3_8.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 167 entries, 0 to 166
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Hole 167 non-null object
1 From 167 non-null float64
2 Len 159 non-null float64
3 Den 167 non-null float64
4 Vp 167 non-null float64
5 Vs 167 non-null float64
6 Mag 167 non-null float64
7 Ip 167 non-null float64
8 Res 167 non-null float64
9 Form 167 non-null object
10 GR 167 non-null float64
dtypes: float64(9), object(2)
memory usage: 14.5+ KB
Modeling¶
Having the GR already integrated into the petrophysical data of borehole TC-3660-008 we are ready for modeling, which involves a regression analysis to generate predictive numerical outputs. The steps required are:
Split the data for training and test or evaluation
Select and run the regression models
Test or evaluate the results of the different models
With the best ML algorithm, generate a synthetic GR for borehole TC-1319-005
Data Split¶
Here we selected the petrophysical features and target (GR) in borehole TC-3660-008 for modeling, leaving 20% (34) of them aside for testing or evaluation of the regression algorithms.
features for modeling
features_model_8 = features3_8.drop(columns=['Hole', 'Len', 'Form', 'GR'])
print(features_model_8.shape)
features_model_8.head()
(167, 7)
target or objetive
target_8 = features3_8.GR
target_8
0 30.578377
1 30.455095
2 34.024174
3 23.740136
4 24.472588
...
162 59.538951
163 76.511278
164 68.944642
165 77.107392
166 76.615594
Name: GR, Length: 167, dtype: float64
Split and shape of data for training and testing
X_train, X_test, y_train, y_test = train_test_split(features_model_8, target_8, test_size=0.2, random_state=seed)
# X_train = np.array(X_train).flatten()
# y_train = np.array(y_train).flatten()
print('X_train shape:', X_train.shape)
print('y_train shape:', y_train.shape)
print('X_test shape:', X_test.shape)
print('y_test shape:', y_test.shape)
X_train shape: (133, 7)
y_train shape: (133,)
X_test shape: (34, 7)
y_test shape: (34,)
- Regression Models
In this analysis, we trained and evaluated nine regression models, some of which are influenced by random processes (those using the random_state=seed argument). After testing with different seed values (e.g., 123, 456, 789), we observed variations in the top-performing model, typically alternating between Gradient Boosting, Extreme Gradient Boosting, and Random Forest. To mitigate this variability and ensure a more reliable evaluation, we implemented cross-validation for the calculation of the metrics.
Regression models and metrics with a fixed seed
seed = 123
models = []
models.append(('LR', LinearRegression()))
models.append(('L', Lasso()))
models.append(('R', Ridge()))
models.append(('SVR', SVR()))
models.append(('KNR', KNeighborsRegressor()))
models.append(('GB', GradientBoostingRegressor(random_state=seed)))
models.append(('DTR', DecisionTreeRegressor(random_state=seed)))
models.append(('RFR', RandomForestRegressor(random_state=seed)))
models.append(('XGB', xgb.XGBRegressor(objective ='reg:squarederror')))
headers = ['Model', 'Sum of Residuals', 'MAE', 'MSE', 'RMSE', 'R2']
rows = []
for name, model in models:
model.fit(X_train, y_train)
predict = model.predict(X_test)
sum_residual = sum(y_test - predict)
mae = mean_absolute_error(y_test, predict)
mse = mean_squared_error(y_test, predict)
rmse = np.sqrt(mse)
score = model.score(X_test, y_test)
rows.append([name, sum_residual, mae, mse, rmse, score])
print('Seed:', seed)
print(tabulate(rows, headers=headers, tablefmt="fancy_outline"))
Seed: 123
╒═════════╤═════════════════════╤══════════╤══════════╤══════════╤════════════╕
│ Model │ Sum of Residuals │ MAE │ MSE │ RMSE │ R2 │
╞═════════╪═════════════════════╪══════════╪══════════╪══════════╪════════════╡
│ LR │ -4.86117 │ 8.93602 │ 129.384 │ 11.3747 │ 0.230243 │
│ L │ 11.9249 │ 8.86367 │ 136.354 │ 11.6771 │ 0.188777 │
│ R │ 9.17722 │ 8.87722 │ 135.115 │ 11.6239 │ 0.196147 │
│ SVR │ 165.92 │ 10.0965 │ 182.715 │ 13.5172 │ -0.0870428 │
│ KNR │ 44.6092 │ 8.80595 │ 153.988 │ 12.4092 │ 0.0838649 │
│ GB │ -18.2136 │ 7.03068 │ 73.9925 │ 8.60189 │ 0.55979 │
│ DTR │ -34.3359 │ 12.1705 │ 210.477 │ 14.5078 │ -0.252209 │
│ RFR │ -11.9149 │ 7.9933 │ 100.311 │ 10.0155 │ 0.403212 │
│ XGB │ -55.5957 │ 7.40284 │ 82.3656 │ 9.07555 │ 0.509975 │
╘═════════╧═════════════════════╧══════════╧══════════╧══════════╧════════════╛
Regression models and metrics with a fixed seed and cross-validation
seed = 123
models = []
models.append(('LR', LinearRegression()))
models.append(('L', Lasso()))
models.append(('R', Ridge()))
models.append(('SVR', SVR()))
models.append(('KNR', KNeighborsRegressor()))
models.append(('GB', GradientBoostingRegressor(random_state=seed)))
models.append(('DTR', DecisionTreeRegressor(random_state=seed)))
models.append(('RFR', RandomForestRegressor(random_state=seed)))
models.append(('XGB', xgb.XGBRegressor(objective ='reg:squarederror')))
headers = ['Model', 'MAE', 'MSE', 'RMSE', 'R2']
rows = []
n_folds = 5
rmse_scorer = make_scorer(lambda y_true, y_pred: np.sqrt(mean_squared_error(y_true, y_pred)))
for name, model in models:
scores_mae = cross_val_score(model, X_train, y_train, cv=n_folds, scoring='neg_mean_absolute_error')
scores_mse = cross_val_score(model, X_train, y_train, cv=n_folds, scoring='neg_mean_squared_error')
scores_rmse = cross_val_score(model, X_train, y_train, cv=n_folds, scoring=rmse_scorer)
scores_r2 = cross_val_score(model, X_train, y_train, cv=n_folds, scoring='r2')
mae = -np.mean(scores_mae)
mse = -np.mean(scores_mse)
rmse = np.mean(scores_rmse)
r2 = np.mean(scores_r2)
rows.append([name, mae, mse, rmse, r2])
print('Seed:', seed)
print(tabulate(rows, headers=headers, tablefmt="fancy_outline"))
Seed: 123
╒═════════╤═════════╤══════════╤══════════╤═══════════╕
│ Model │ MAE │ MSE │ RMSE │ R2 │
╞═════════╪═════════╪══════════╪══════════╪═══════════╡
│ LR │ 7.11785 │ 92.1091 │ 9.4983 │ 0.268285 │
│ L │ 7.30283 │ 94.0936 │ 9.60407 │ 0.252065 │
│ R │ 7.2349 │ 93.1695 │ 9.55375 │ 0.259637 │
│ SVR │ 7.88615 │ 124.49 │ 11.1176 │ 0.0328943 │
│ KNR │ 8.07405 │ 114.013 │ 10.6201 │ 0.106625 │
│ GB │ 7.14677 │ 104.942 │ 10.1178 │ 0.183119 │
│ DTR │ 8.12116 │ 128.029 │ 11.1078 │ 0.0187 │
│ RFR │ 7.31101 │ 97.9016 │ 9.80004 │ 0.230271 │
│ XGB │ 7.08965 │ 100.852 │ 9.96463 │ 0.195461 │
╘═════════╧═════════╧══════════╧══════════╧═══════════╛
Best Regression Model¶
After applying cross-validation, Linear Regression (LR) emerged as the top-performing model with an R² of 0.265, followed by Ridge Regression (R) with an R² of 0.256, and Lasso Regression (L) with an R² of 0.247.
Next, we selected features from borehole C-1319-005 to predict GR, based on the best model trained on borehole TC-3660-008. The chosen model is LR, with additional predictions generated using XGB.
Petrophysical features of borehole TC-1319-005
features3_5 = features3[features3.Hole=='TC-1319-005']
features3_5 = features3_5.reset_index(drop=True)
features3_5
Petrophysical features of borehole TC-1319-005 for modeling
features_model_5 = features3_5.drop(columns=['Hole', 'Len', 'Form'])
print(features_model_5.shape)
features_model_5.head()
(161, 7)
GR by Linear Regressor
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)
gr5_lr = lr_model.predict(features_model_5)
gr5_lr
array([37.48012316, 40.29644384, 23.09190308, 44.8346237 , 27.11026391,
35.69517186, 35.80346419, 42.98681624, 21.71842209, 50.42072407,
43.10646152, 42.64311325, 36.81285745, 35.75724267, 24.77325061,
38.88608028, 18.99647974, 18.34440846, 24.71733796, 49.77336379,
31.50291417, 50.27812368, 12.68860118, 40.97470383, 41.35654788,
9.46749403, 45.41312187, 57.11531171, 52.44942385, 55.00547771,
54.99299988, 58.31717629, 63.00910746, 38.18780739, 43.40488394,
53.54787669, 38.28788144, 54.77673522, 53.94068928, 50.00196899,
53.33280443, 51.97077575, 43.94754544, 44.7692286 , 55.2820785 ,
42.99287884, 43.53616197, 43.90804534, 45.1923788 , 43.3995711 ,
52.41320378, 38.40547193, 49.45734775, 54.47626681, 35.21860407,
40.97396549, 44.98800414, 52.50782359, 33.17683036, 56.93967984,
31.80814629, 38.25475496, 58.61926752, 46.56422313, 55.22333646,
48.95181455, 56.40445626, 56.21276624, 40.55208937, 44.54711027,
34.30283305, 41.41804912, 56.44581239, 50.82112976, 38.51075176,
42.79861258, 45.19983303, 50.65237446, 38.59099861, 52.70893187,
48.80542021, 42.14681373, 62.89384827, 46.03558981, 41.10928562,
48.24311094, 41.97767837, 45.75722795, 48.64259008, 48.654642 ,
45.50473295, 40.33085351, 44.94789532, 43.92711492, 44.22012991,
49.9342732 , 60.21970233, 62.67858876, 62.02673151, 52.49919054,
46.20133463, 50.31771774, 44.34999683, 54.34472837, 32.06757116,
46.52112522, 66.25802377, 58.53394378, 55.59449825, 61.29707256,
51.95505826, 53.61999492, 51.86700364, 54.94377794, 54.86303988,
59.14183574, 66.23808415, 55.51343349, 59.19185001, 52.3024468 ,
48.61038302, 64.82166153, 46.11411479, 64.31701643, 63.04114529,
52.15649911, 56.70399617, 51.08228262, 65.68280901, 59.08239203,
51.20549995, 38.84526869, 62.50110662, 48.03486534, 54.3338539 ,
53.59520789, 51.58907318, 51.19657462, 53.01946386, 47.82961527,
71.89787018, 65.52042076, 54.58325456, 51.06668569, 68.48469698,
64.49554711, 48.54356557, 51.14052389, 51.62244032, 50.396638 ,
59.06133645, 68.13949395, 75.84718351, 74.02208004, 62.65090578,
71.2700738 , 67.4500938 , 69.8234084 , 61.83761112, 64.01707194,
64.17237329])
GR by Extreme Gradient Boosting Regressor
xgb_model = xgb.XGBRegressor(objective ='reg:squarederror')
xgb_model.fit(X_train, y_train)
gr5_xgb = xgb_model.predict(features_model_5)
gr5_xgb
array([34.75164 , 40.796104, 36.992447, 42.021427, 35.146862, 32.735653,
31.437817, 44.679855, 25.369324, 37.394672, 37.02685 , 34.253475,
41.54279 , 35.28796 , 37.156284, 27.499958, 24.900589, 59.073536,
25.334816, 33.707527, 30.582035, 36.551727, 58.758087, 39.717037,
37.68949 , 51.238953, 37.855713, 37.301083, 36.851 , 33.767624,
33.657173, 35.071648, 39.557102, 36.829685, 33.846024, 37.697605,
37.730824, 34.91515 , 36.3279 , 38.628242, 37.983574, 38.069294,
38.160236, 38.536686, 38.399925, 38.082027, 39.27452 , 37.119156,
39.841293, 45.398674, 35.81751 , 38.662144, 35.173935, 34.593754,
33.010708, 39.53115 , 39.431847, 41.398838, 35.45763 , 35.191555,
34.551064, 31.259857, 38.560356, 37.284836, 41.16499 , 38.056583,
41.03737 , 35.434082, 38.705368, 39.224365, 36.462032, 36.3096 ,
36.547577, 45.77963 , 41.261803, 33.92088 , 34.588528, 39.656155,
39.15763 , 37.552555, 38.922432, 39.36756 , 38.62001 , 38.477215,
41.59901 , 40.979454, 47.4265 , 53.00436 , 54.575684, 48.65887 ,
52.29925 , 49.431183, 51.90922 , 49.391224, 52.66824 , 49.652584,
48.35062 , 44.88772 , 53.68105 , 40.471123, 49.45793 , 51.189827,
48.084194, 53.25084 , 50.381542, 59.261337, 65.46839 , 41.859623,
46.78074 , 45.050728, 41.25792 , 49.75928 , 49.73571 , 60.701645,
60.768967, 61.67022 , 61.20107 , 61.175545, 61.259388, 56.77341 ,
55.918613, 51.66773 , 54.700287, 54.94038 , 57.015076, 53.717358,
53.812485, 66.552025, 67.536354, 56.427017, 57.21038 , 49.67948 ,
54.108974, 54.36197 , 55.57285 , 53.881783, 55.802116, 55.35852 ,
54.312916, 55.4986 , 62.86732 , 53.801105, 54.689976, 54.729584,
51.35334 , 66.19035 , 68.41729 , 55.093616, 68.71511 , 56.620056,
53.18428 , 55.686577, 52.945896, 52.141483, 55.897858, 50.89671 ,
54.226032, 51.24211 , 68.31796 , 50.653297, 74.86713 ],
dtype=float32)
Merge the two synthetic GRs into the petrophysical data of borehole TC-1319-005
features3_5['GR_lr'], features3_5['GR_xgb'] = gr5_lr, gr5_xgb
features3_5
There are no NaNs in the merge data of borehole TC-1319-005
features3_5.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 161 entries, 0 to 160
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Hole 161 non-null object
1 From 161 non-null float64
2 Len 161 non-null float64
3 Den 161 non-null float64
4 Vp 161 non-null float64
5 Vs 161 non-null float64
6 Mag 161 non-null float64
7 Ip 161 non-null float64
8 Res 161 non-null float64
9 Form 161 non-null object
10 GR_lr 161 non-null float64
11 GR_xgb 161 non-null float32
dtypes: float32(1), float64(9), object(2)
memory usage: 14.6+ KB
Understanding the Model¶
Beyond determining which regression model performs better, it is important to examine the coefficients of the Linear Regression (LR) model to understand the relative importance and influence of each feature. The magnitude and sign of these coefficients reveal which features contribute most to the target, whether positively or negatively.
The table and plot below (negative coefficients were inverted for the logarithm, and colored in red) show that Den has a strong negative impact, while Mag has a significant positive effect. In contrast, Vp, Vs, and Ip have much smaller impacts, and the influence of Res is insignificant. The intercept represents the baseline value when all features are zero.
X_train
Linear regressor coefficients
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)
print('Features:', X_train.columns, '\n')
print("Coeficientes:", lr_model.coef_, '\n')
print("Intercepto:", lr_model.intercept_)
Features: Index(['From', 'Den', 'Vp', 'Vs', 'Mag', 'Ip', 'Res'], dtype='object')
Coeficientes: [ 2.27539299e-02 -3.56367531e+01 4.98929080e-03 -1.28090298e-02
1.19706930e+01 7.13230615e-02 1.08666969e-04]
Intercepto: 130.7206610710383
Linear regressor coefficients in table
features_list = list(X_train.columns)
features_list.append('Intercepto')
coef_list = list(lr_model.coef_)
coef_list.append(lr_model.intercept_)
table = list(zip(features_list, coef_list))
print(tabulate(table, headers=['Feature', 'Coefficient'], tablefmt="fancy_outline"))
╒════════════╤═══════════════╕
│ Feature │ Coefficient │
╞════════════╪═══════════════╡
│ From │ 0.0227539 │
│ Den │ -35.6368 │
│ Vp │ 0.00498929 │
│ Vs │ -0.012809 │
│ Mag │ 11.9707 │
│ Ip │ 0.0713231 │
│ Res │ 0.000108667 │
│ Intercepto │ 130.721 │
╘════════════╧═══════════════╛
Linear regressor coefficients in linear and log10 plot
plt.figure(figsize=(13,5))
plt.subplot(121)
plt.bar(features_list, (coef_list), label='Positive')
plt.bar(features_list[1], (coef_list[1]), color='r', label='negative')
plt.legend()
plt.ylabel('Coeficients')
plt.grid()
plt.subplot(122)
plt.bar(features_list, np.log10(coef_list))
plt.bar(features_list[1], np.log10(-coef_list[1]), color='r')
plt.bar(features_list[3], np.log10(-coef_list[3]), color='r')
plt.ylabel('Log10[Coeficients]')
plt.grid()
plt.tight_layout;
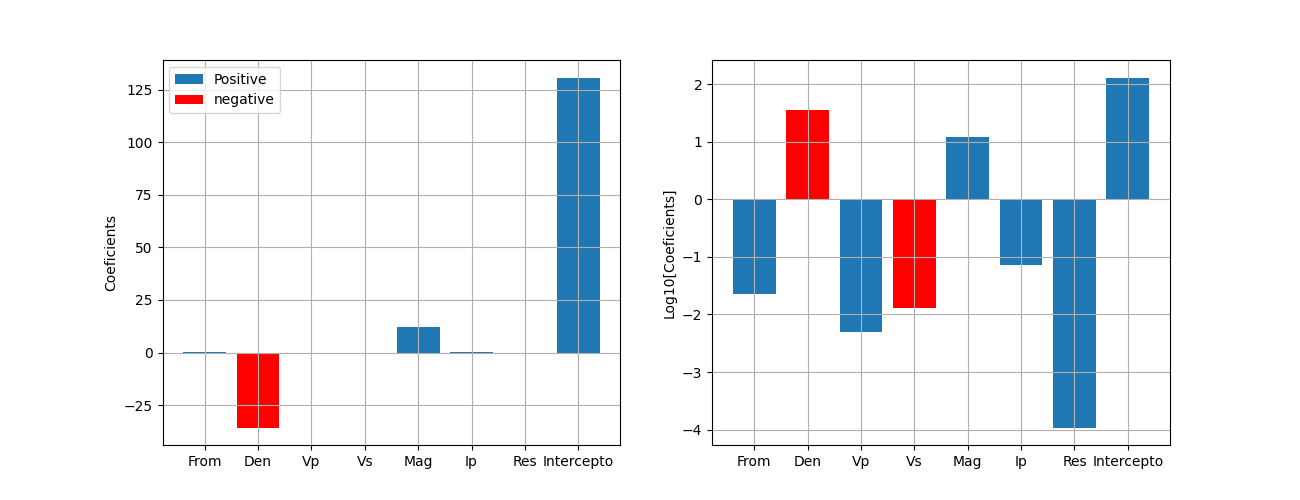
<function tight_layout at 0x7f32d4e31360>
Graphic Comparison¶
The legacy GR data and major formation tops from borehole TC-3660-008 were integrated in the first notebook (1/3), provide a reference for comparing the new ML-generated GRs in borehole TC-1319-005. While the Linear Regression (LR) model achieved a higher R² score, the GR predictions generated by the XGB model (with an R² of only 0.170) more closely follow the patterns observed in the reference borehole TC-3660-008.
The original and ML-generated GRs are presented in the plot at the end of the section. To make the comparison easier between both ML-generated GRs, the GR generated by the XGB algorithm (in orange) was displayed to the right by adding 40 API units.
Load of tops from borehole TC-3660-008
# Leer el archivo JSON
with open(f'{base_path}/tops_list_8.json', 'r') as json_file:
tops_list_8 = json.load(json_file)
tops_list_8
[{'name': 'CALP', 'top': 9.6, 'base': 270.95, 'color': '#CCDF9A'}, {'name': 'FLT', 'top': 270.95, 'base': 304.3, 'color': '#FF0000'}, {'name': 'CALP', 'top': 304.3, 'base': 345.9, 'color': '#CCDF9A'}, {'name': 'VISS', 'top': 345.9, 'base': 363.8, 'color': '#D9E9F0'}, {'name': 'FLT', 'top': 363.8, 'base': 369.26, 'color': '#FF0000'}, {'name': 'VISS', 'top': 369.26, 'base': 399.33, 'color': '#D9E9F0'}, {'name': 'FLT', 'top': 399.33, 'base': 401.88, 'color': '#FF0000'}, {'name': 'VISS', 'top': 401.88, 'base': 424.46, 'color': '#D9E9F0'}, {'name': 'FLT', 'top': 424.46, 'base': 460.16, 'color': '#FF0000'}, {'name': 'S', 'top': 460.16, 'base': 504.62, 'color': '#8CBAE2'}, {'name': 'LABL', 'top': 504.62, 'base': 724.5, 'color': '#8A6E9F'}, {'name': 'SP', 'top': 724.5, 'base': 785.08, 'color': '#ABA16C'}, {'name': 'P', 'top': 785.08, 'base': 814.55, 'color': '#EBDE98'}, {'name': 'LIS', 'top': 814.55, 'base': 825.6, 'color': '#806000'}, {'name': 'PAL', 'top': 825.6, 'base': 833.5, 'color': '#2A7C43'}]
Tops in borehole TC-1319-005
features3_5.Form.unique()
array(['CALP', 'LABL', 'SP', 'P', 'LIS', 'PAL'], dtype=object)
Extraction of top depths in borehole TC-1319-005
tops5 = pd.DataFrame(features3_5.From[features3_5.Form.ne(features3_5.Form.shift())])
tops5
Extraction tops names in borehole TC-1319-005
tops5['Top'] = features3_5.Form[features3_5.Form.ne(features3_5.Form.shift())]
tops5
Reset of indexes
tops5 = tops5.reset_index(drop=True)
tops5
Colors of the formations in borehole TC-1319-005
tops5['color'] = pd.Series([ '#CCDF9A', '#8A6E9F', '#ABA16C', '#EBDE98', '#806000', '#2A7C43'])
tops5
Bottom of the last formation
new_row5 = pd.DataFrame([{'From':1059.20, 'Top': '', 'color':''}])
new_row5
Merge of dataframes
tops5 = pd.concat([tops5, new_row5], ignore_index=True)
tops5
Rename of columns of the dataframe
tops5 = tops5.rename(columns={'From':'depth', 'Top':'name'})
tops5
Convertion of the dataframe to a list of dictionaries by UDL, borehole TC-1319-005
tops_list_5 = geo.plot_tops(tops5)
tops_list_5
[{'name': 'CALP', 'top': np.float64(265.77), 'base': np.float64(503.4), 'color': '#CCDF9A'}, {'name': 'LABL', 'top': np.float64(503.4), 'base': np.float64(830.45), 'color': '#8A6E9F'}, {'name': 'SP', 'top': np.float64(830.45), 'base': np.float64(911.1), 'color': '#ABA16C'}, {'name': 'P', 'top': np.float64(911.1), 'base': np.float64(1038.37), 'color': '#EBDE98'}, {'name': 'LIS', 'top': np.float64(1038.37), 'base': np.float64(1049.2), 'color': '#806000'}, {'name': 'PAL', 'top': np.float64(1049.2), 'base': np.float64(1059.2), 'color': '#2A7C43'}]
Saving the tops to a json file
with open('Output/tops_list_5.json', 'w') as json_file:
json.dump(tops_list_5, json_file, indent=4)
Plot of GRs with formations
plt.figure(figsize=(10, 8))
plt.subplot(141)
plt.plot(gr8.iloc[:,1], gr8.iloc[:,0], label='Real', c='lightblue')
# plt.plot(gr8.iloc[:,2].rolling(window=250).mean(), gr8.iloc[:,1], label='Mean 400')
plt.xlabel('GR (API)')
# Butterworth filter
b, a = butter(N=2, Wn=0.02, btype='low')
filtered_data = filtfilt(b, a, gr8.iloc[:,1])
plt.plot(filtered_data, gr8.iloc[:,0], label='BWF')
plt.legend()
plt.grid()
plt.xlabel('GR (API)')
plt.ylabel('Depth (m)')
plt.axis([0, 120, 1100, 0])
plt.subplot(142)
for i in range(0, len(tops_list_8)):
plt.axhspan(tops_list_8[i]['top'], tops_list_8[i]['base'], color=tops_list_8[i]['color'])
plt.text(122, tops_list_8[i]['top'], tops_list_8[i]['name'], fontsize=6, va='center')
plt.axis([0, 120, 1100, 0])
plt.xticks([])
plt.xlabel('Formations')
plt.subplot(143)
plt.plot(features3_5.GR_lr, features3_5.From, label='LR')
plt.plot(features3_5.GR_xgb + 40, features3_5.From, label='XGB + 40')
plt.legend()
plt.grid()
plt.xlabel('GR (API)')
plt.axis([0, 120, 1100, 0])
plt.subplot(144)
for i in range(0, len(tops_list_5)):
plt.axhspan(tops_list_5[i]['top'], tops_list_5[i]['base'], color=tops_list_5[i]['color'])
plt.text(122, tops_list_5[i]['top'], tops_list_5[i]['name'], fontsize=7, va='center')
plt.axis([0, 120, 1100, 0])
plt.xticks([])
plt.xlabel('Formations')
plt.suptitle('GR and Formations in Boreholes\nTC-3660-008 TC-1319-005', y=0.98)
plt.tight_layout()
plt.savefig('Output/all_grs.png', dpi=300)
plt.show()
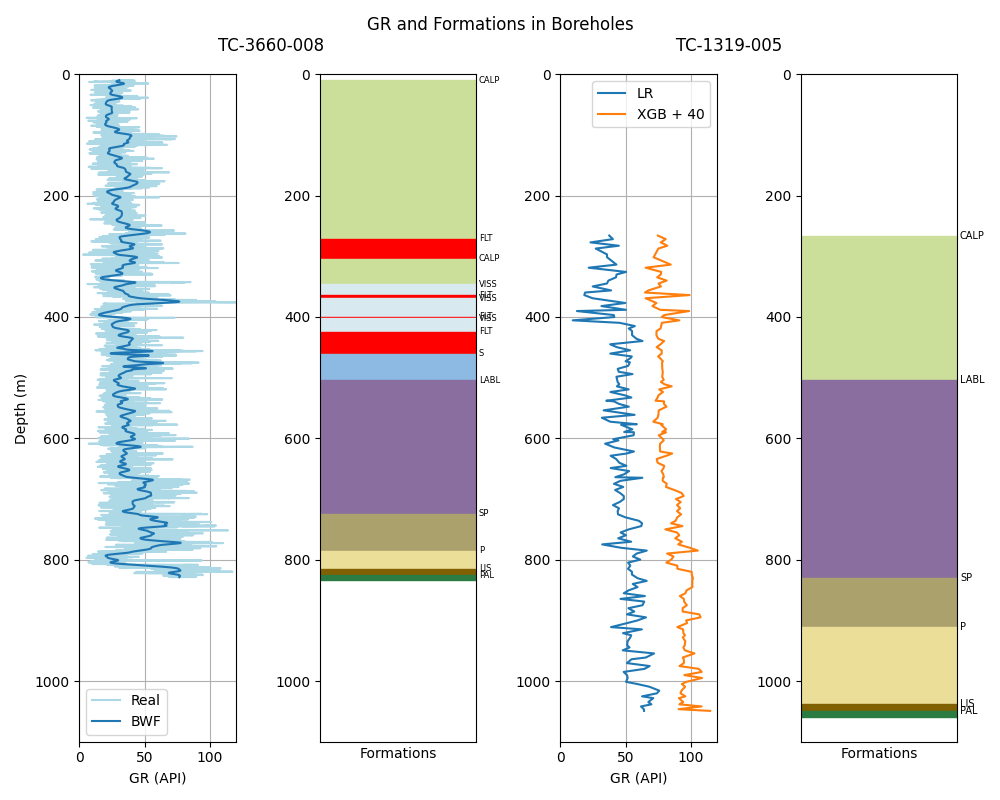
Observations¶
Here are some observations related to the tasks covered in this notebook:
This notebook highlights the utility of open-source Python tools in addressing the issue of incomplete and sparse petrophysical data in mining. The various regression models employed demonstrate that machine learning techniques can be effective in filling data gaps, even when direct measurements are limited or unavailable.
More complex models, such as Extreme Gradient Boosting, provided higher predictive accuracy following the pattern of the reference GR, but simpler models like Linear Regression offered better interpretability. This trade-off between accuracy and interpretability is a crucial consideration for practical applications in mining data analysis.
The coefficients in the Linear Regression model indicated that variables such as Den and Mag significantly impact the target variable (GR), demonstrating strong correlation and critical predictive roles in petrophysical properties. In contrast, Vp and Res were less important, contributing minimally to the model’s predictions.
Final Remarks¶
The analysis of the petrophysical dataset from Collinstown highlights challenges related to data dispersion and scarcity, as well as the potential of machine learning (ML) tools to enhance the value of mining data.
Data dispersion, particularly in Den and Vp, complicates the generation of accurate models and reflects the inherent heterogeneity of the subsurface. Variations across boreholes and core samples, along with some false anomalies from measurement issues, must be addressed to ensure data integrity and reliable modeling. Low correlation (or low covariance) in the dataset, resulting from fractures and methodological limitations, leads to models with low R² values.
ML algorithms and Python-based tools have proven valuable for integrating legacy data with new sources, thereby improving dataset quality. Techniques such as imputation and regression modeling help fill gaps and enhance the resolution of petrophysical properties. Overall, ML tools present significant opportunities to improve legacy data and support its integration with new datasets, leading to more accurate mining models.
Both this analysis and the previous notebook demonstrate the effective use of open-source Python tools and ML models to address incomplete and sparse petrophysical data in mining exploration. This adaptable workflow can be applied across various geological contexts, benefiting other mining projects as well.
Next Steps¶
Here are some possible next steps to build on the work from this and the previous notebooks:
Consider exploring classification models, especially if there is interest in classifying different types of rocks or deposits based on petrophysical properties rather than predicting continuous variables.
Explore advanced feature engineering or transformation techniques to uncover more complex relationships between variables. This could potentially improve the model’s performance.
Further optimize the machine learning models by performing hyperparameter tuning. This can improve the accuracy of the predictions and refine the model selection process.
Apply the propagation of missing properties using the models obtained here to other boreholes with limited data.
These steps would extend the current analysis, enhance model accuracy, and contribute to more practical applications in mining exploration.
Total running time of the script: (0 minutes 3.688 seconds)
